Another Word For It Patrick Durusau on Topic Maps and Semantic Diversity

January 23, 2018

The vector algebra war: a historical perspective [Semantic Confusion in Engineering and Physics]

Filed under: Algebra,Mathematics,Semantic Diversity,Semantic Inconsistency,Semantics,Topic Maps — Patrick Durusau @ 8:33 pm

The vector algebra war: a historical perspective by James M. Chappell, Azhar Iqbal, John G. Hartnett, Derek Abbott.

Abstract:

There are a wide variety of different vector formalisms currently utilized in engineering and physics. For example, Gibbs’ three-vectors, Minkowski four-vectors, complex spinors in quantum mechanics, quaternions used to describe rigid body rotations and vectors defined in Clifford geometric algebra. With such a range of vector formalisms in use, it thus appears that there is as yet no general agreement on a vector formalism suitable for science as a whole. This is surprising, in that, one of the primary goals of nineteenth century science was to suitably describe vectors in three-dimensional space. This situation has also had the unfortunate consequence of fragmenting knowledge across many disciplines, and requiring a significant amount of time and effort in learning the various formalisms. We thus historically review the development of our various vector systems and conclude that Clifford’s multivectors best fulfills the goal of describing vectorial quantities in three dimensions and providing a unified vector system for science.

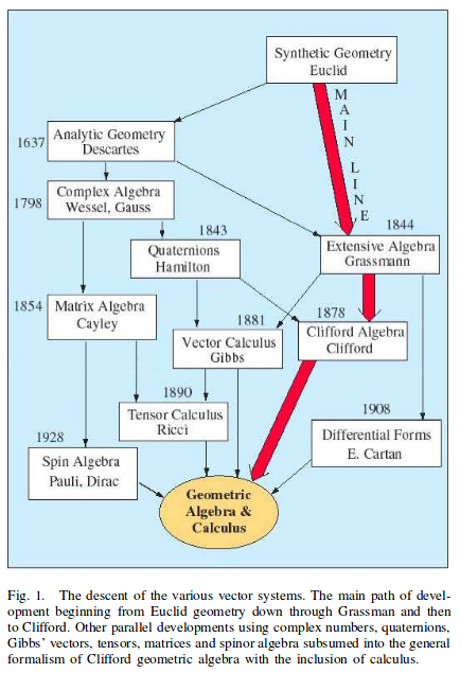
An image from the paper captures the “descent of the various vector systems:”

The authors contend for use of Clifford’s multivectors over the other vector formalisms described.

Assuming Clifford’s multivectors displace all other systems in use, the authors fail to answer how readers will access the present and past legacy of materials in other formalisms?

If the goal is to eliminate “fragmenting knowledge across many disciplines, and requiring a significant amount of time and effort in learning the various formalisms,” that fails in the absence of a mechanism to access existing materials using the Clifford’s multivector formalism.

Topic maps anyone?

May 21, 2017

immersive linear algebra

Filed under: Algebra,Mathematics — Patrick Durusau @ 4:56 pm

immersive linear algebra by J. Ström, K. Åström, and T. Akenine-Möller.

Billed as:

The world’s first linear algebra book with fully interactive figures.

From the preface:

“A picture says more than a thousand words” is a common expression, and for text books, it is often the case that a figure or an illustration can replace a large number of words as well. However, we believe that an interactive illustration can say even more, and that is why we have decided to build our linear algebra book around such illustrations. We believe that these figures make it easier and faster to digest and to learn linear algebra (which would be the case for many other mathematical books as well, for that matter). In addition, we have added some more features (e.g., popup windows for common linear algebra terms) to our book, and we believe that those features will make it easier and faster to read and understand as well.

After using linear algebra for 20 years times three persons, we were ready to write a linear algebra book that we think will make it substantially easier to learn and to teach linear algebra. In addition, the technology of mobile devices and web browsers have improved beyond a certain threshold, so that this book could be put together in a very novel and innovative way (we think). The idea is to start each chapter with an intuitive concrete example that practically shows how the math works using interactive illustrations. After that, the more formal math is introduced, and the concepts are generalized and sometimes made more abstract. We believe it is easier to understand the entire topic of linear algebra with a simple and concrete example cemented into the reader’s mind in the beginning of each chapter.

Please contact us if there are errors to report, things that you think should be improved, or if you have ideas for better exercises etc. We sincerely look forward to hearing from you, and we will continuously improve this book, and add contributing people to the acknowledgement.
… (popups omitted)

Unlike some standards I could mention, but won’t, the authors number just about everything, making it easy to reference equations, illustrations, etc.

Enjoy!

November 24, 2015

Graphical Linear Algebra

Filed under: Algebra,Mathematics — Patrick Durusau @ 5:49 pm

Graphical Linear Algebra by Pawel Sobocinski.

From Episode 1, Makélélé and Linear Algebra.

Linear algebra is the Claude Makélélé of science and mathematics. Makélélé is a well-known, retired football player, a French international. He played in the famous Real Madrid team of the early 2000s. That team was full of “galácticos” — the most famous and glamorous players of their generation. Players like Zidane, Figo, Ronaldo and Roberto Carlos. Makélélé was hardly ever in the spotlight, he was paid less than his more celebrated colleagues and was frequently criticised by fans and journalists. His style of playing wasn’t glamorous. To the casual fan, there wasn’t much to get excited about: he didn’t score goals, he played boring, unimaginative, short sideways passes, he hardly ever featured in match highlights. In 2003 he signed for Chelsea for relatively little money, and many Madrid fans cheered. But their team started losing matches.

The importance of Makélélé’s role was difficult to appreciate for the non-specialist. But football insiders regularly described him as the work-horse, the engine room, the battery of the team. He sat deep in midfield, was always in the right place to disrupt opposition attacks, recovered possession, and got the ball out quickly to his teammates, turning defence into attack. Without Makélélé, the galácticos didn’t look quite so galactic.

Similarly, linear algebra does not get very much time in the spotlight. But many galáctico subjects of modern scientific research: e.g. artificial intelligence and machine learning, control theory, solving systems of differential equations, computer graphics, “big data“, and even quantum computing have a dirty secret: their engine rooms are powered by linear algebra.

Linear algebra is not very glamorous. It is normally taught to science undergraduates in their first year, to prepare for the more exciting stuff ahead. It is background knowledge. Everyone has to learn what a matrix is, and how to add and multiply matrices.
…

I have only read the first three or four posts but Pawel’s post look like a good way to refresh or acquire a “background” in linear algebra.

Math is important for “big data” and as Renee Teate reminded us in A Challenge to Data Scientists, bias can be lurking anywhere, data, algorithms, us, etc.

Or as I am fond of saying, “if you let me pick the data or the algorithm, I can produce a specified result, every time.”

Bear that in mind when someone tries to hurry past your questions about data, its acquisition, processing before you saw it, and/or wanting to know the details of an algorithm and how it was applied.

There’s a reason why people want to gloss over such matters and the answer isn’t a happy one, at least from the questioner’s perspective.

Refresh or get an background in linear algebra!

The more you know, the less vulnerable you will be to manipulation and/or fraud.

I first saw this in a tweet by Algebra Fact.

August 20, 2014

Math for machine learning

Filed under: Algebra,Machine Learning,Mathematics — Patrick Durusau @ 7:36 pm

Math for machine learning by Zygmunt Zając.

From the post:

Sometimes people ask what math they need for machine learning. The answer depends on what you want to do, but in short our opinion is that it is good to have some familiarity with linear algebra and multivariate differentiation.

Linear algebra is a cornerstone because everything in machine learning is a vector or a matrix. Dot products, distance, matrix factorization, eigenvalues etc. come up all the time.

Differentiation matters because of gradient descent. Again, gradient descent is almost everywhere*. It found its way even into the tree domain in the form of gradient boosting – a gradient descent in function space.

We file probability under statistics and that’s why we don’t mention it here.
…

Following this introduction you will find a series of books, MOOCs, etc. on linear algebra, calculus and other math resources.

Pass it along!

July 28, 2014

Abstract Algebra, Category Theory, Haskell

Filed under: Algebra,Category Theory,Functional Programming,Haskell — Patrick Durusau @ 3:09 pm

Abstract Algebra, Category Theory, Haskell: Recommended Reading Material

A great annotated reading list for Abstract Algebra, Category Theory, and Haskell.

As an added feature, there are links to the cited works on Google Books. You won’t be able to see entire works but enough to choose between them.

July 13, 2014

Abstract Algebra

Filed under: Algebra,Mathematics — Patrick Durusau @ 7:19 pm

Abstract Algebra by Benedict Gross, PhD, George Vasmer Leverett Professor of Mathematics, Harvard University.

From the webpage:

Algebra is the language of modern mathematics. This course introduces students to that language through a study of groups, group actions, vector spaces, linear algebra, and the theory of fields.

Videos, notes, problem sets from the Harvard Extension School.

The relationship between these videos and those found on YouTube isn’t clear.

The text book for the class was Algebra by Michael Artin. (There is a 2nd edition now.)

There are two comments that may motivate you to pursue these lectures:

First, Gross remarks in the first session that there are numerous homework assignments because you are learning a language. Which makes me curious why math isn’t taught like a language?

Second, the Wikipedia article on abstract algebra observes in part:

Numerous textbooks in abstract algebra start with axiomatic definitions of various algebraic structures and then proceed to establish their properties. This creates a false impression that in algebra axioms had come first and then served as a motivation and as a basis of further study. The true order of historical development was almost exactly the opposite. For example, the hypercomplex numbers of the nineteenth century had kinematic and physical motivations but challenged comprehension. Most theories that are now recognized as parts of algebra started as collections of disparate facts from various branches of mathematics, acquired a common theme that served as a core around which various results were grouped, and finally became unified on a basis of a common set of concepts. An archetypical example of this progressive synthesis can be seen in the history of group theory.

Interesting that techniques are developed for quite practical reasons but later justified with greater formality.

Suggests that semantic integration should focus on practical results and leave formal justification for later.

Yes?

I first saw this in a tweet by Steven Strogatz.

May 17, 2014

The Algebra of Algebraic Data Types

Filed under: Algebra,Data Types — Patrick Durusau @ 3:52 pm

Chris Taylor has a series of posts that correspond to a talk he gave in London (November 2012), video on YouTube and slides on Github.

Part 1.

Part 2.

Part 3.

Suggest you read the blog posts first and then following the slides while listening to the video.

If you have been wondering about types in Haskell, this is a golden opportunity.

April 20, 2014

Group Explorer 2.2

Filed under: Algebra,Group Theory,Mathematics — Patrick Durusau @ 11:01 am

Group Explorer 2.2

From the webpage:

Primary features listed here, or read the version 2.2 release notes.

  • Displays Cayley diagrams, multiplication tables, cycle graphs, and objects with symmetry
  • Many common group-theoretic computations can be done visually
  • Compare groups and subgroups via morphisms (see illustration below)
  • Browsable, searchable group library
  • Integrated help system (which you can preview on the web)
  • Save and print images at any scale and quality

Are there symmetries in your data?

I first saw this in a tweet by Steven Strogatz.

BTW, Steven also points to this example of using Group Explorer: Cayley diagrams of the first five symmetric groups.

April 5, 2014

Algorithmic Number Theory, Vol. 1: Efficient Algorithms

Filed under: Algebra,Algorithms,Mathematics — Patrick Durusau @ 7:20 pm

Algorithmic Number Theory, Vol. 1: Efficient Algorithms by Eric Bach and Jeffrey Shallit.

From the preface:

This is the first volume of a projected two-volume set on algorithmic number theory, the design and analysis of algorithms for problems from the theory of numbers. This volume focuses primarily on those problems from number theory that admit relatively efficient solutions. The second volume will largely focus on problems for which efficient algorithms are not known, and applications thereof.

We hope that the material in this book will be useful for readers at many levels, from the beginning graduate student to experts in the area. The early chapters assume that the reader is familiar with the topics in an undergraduate algebra course: groups, rings, and fields. Later chapters assume some familiarity with Galois theory.

As stated above, this book discusses the current state of the art in algorithmic number theory. This book is not an elementary number theory textbook, and so we frequently do not give detailed proofs of results whose central focus is not computational. Choosing otherwise would have made this book twice as long.

The webpage offers the BibTeX files for the bibliography, which includes more than 1800 papers and books.

BTW, Amazon notes that Volume 2 was never published.

Now that high performance computing resources are easily available, perhaps you can start working on your own volume 2. Yes?

I first saw this in a tweet by Alvaro Videla.

March 11, 2014

Number Theory and Algebra

Filed under: Algebra,Cryptography,Mathematics — Patrick Durusau @ 6:28 pm

A Computational Introduction to Number Theory and Algebra by Victor Shoup.

The first and second editions, published by Cambridge University Press are available for download under a Creative Commons license.

From the preface of the second edition:

Number theory and algebra play an increasingly significant role in computing and communications, as evidenced by the striking applications of these subjects to such fields as cryptography and coding theory. My goal in writing this book was to provide an introduction to number theory and algebra, with an emphasis on algorithms and applications, that would be accessible to a broad audience. In particular, I wanted to write a book that would be appropriate for typical students in computer science or mathematics who have some amount of general mathematical experience, but without presuming too much specific mathematical knowledge.

Even though reliance on cryptography and vendors of cryptography is fading, you are likely to encounter people still using cryptography or legacy data “protected” by cryptography.

BTW, this is only one of several books that Cambridge University Press has published and allowed the final text to remain available.

Should you pen something appropriate and hopefully profitable for you and a publisher, Cambridge University Press should be on your short list.

Cambridge University Press is a great press and a good citizen of the academic world.
.
I first saw this in a tweet by Algebra Fact.

March 10, 2014

Algebraic and Analytic Programming

Filed under: Algebra,Analytics,Cyc,Mathematics,Ontology,Philosophy,SUMO — Patrick Durusau @ 9:17 am

Algebraic and Analytic Programming by Luke Palmer.

In a short post Luke does a great job contrasting algebraic versus analytic approaches to programming.

In an even shorter summary, I would say the difference is “truth” versus “acceptable results.”

Oddly enough, that difference shows up in other areas as well.

The major ontology projects, including linked data, are pushing one and only one “truth.”

Versus other approaches, such as topic maps (at least in my view), that tend towards “acceptable results.”

I am not sure what other measure of success you would have other than “acceptable results?”

Or what another measure for a semantic technology would be other than “acceptable results?”

Whether the universal truth of the world folks admit it or not, they just have a different definition of “acceptable results.” Their “acceptable results” means their world view.

I appreciate the work they put into their offer but I have to decline. I already have a world view of my own.

You?

I first saw this in a tweet by Computer Science.

February 13, 2014

Algebra for Analytics:…

Filed under: Algebra,Algorithms,Analytics — Patrick Durusau @ 3:44 pm

Algebra for Analytics: Two pieces for scaling computations, ranking and learning by P. Oscar Boykin.

Slide deck from Oscar’s presentation at Strataconf 2014.

I don’t normally say a slide deck on algebra is inspirational but I have to for this one!

Looking forward to watching the video of the presentation that went along with it.

Think of all the things you can do with associativity and hashes before you review the slide deck.

It will make it all the more amazing.

I first saw this in a tweet by Twitter Open Source.

March 12, 2013

A Concise Course in Algebraic Topology

Filed under: Algebra,Mathematics,Topology — Patrick Durusau @ 10:05 am

A Concise Course in Algebraic Topology by J.P. May. (PDF)

From the introduction:

The first year graduate program in mathematics at the University of Chicago consists of three three-quarter courses, in analysis, algebra, and topology. The first two quarters of the topology sequence focus on manifold theory and differential geometry, including differential forms and, usually, a glimpse of de Rham cohomology. The third quarter focuses on algebraic topology. I have been teaching the third quarter off and on since around 1970. Before that, the topologists, including me, thought that it would be impossible to squeeze a serious introduction to algebraic topology into a one quarter course, but we were overruled by the analysts and algebraists, who felt that it was unacceptable for graduate students to obtain their PhDs without having some contact with algebraic topology.

This raises a conundrum. A large number of students at Chicago go into topology, algebraic and geometric. The introductory course should lay the foundations for their later work, but it should also be viable as an introduction to the subject suitable for those going into other branches of mathematics. These notes reflect my efforts to organize the foundations of algebraic topology in a way that caters to both pedagogical goals. There are evident defects from both points of view. A treatment more closely attuned to the needs of algebraic geometers and analysts would include Čech cohomology on the one hand and de Rham cohomology and ˇ perhaps Morse homology on the other. A treatment more closely attuned to the needs of algebraic topologists would include spectral sequences and an array of calculations with them. In the end, the overriding pedagogical goal has been the introduction of basic ideas and methods of thought.

Tough sledding but having insights, like those found in the GraphLab project, require a deeper than usual understanding of the issues at hand.

I first saw this in a tweet by Topology Fact.

November 21, 2012

ALGEBRA, Chapter 0

Filed under: Algebra,Category Theory,Mathematics — Patrick Durusau @ 11:27 am

ALGEBRA, Chapter 0 by Paolo Aluffi. (PDF)

From the introduction:

This text presents an introduction to algebra suitable for upper-level undergraduate or beginning graduate courses. While there is a very extensive offering of textbooks at this level, in my experience teaching this material I have invariably felt the need for a self-contained text that would start ‘from zero’ (in the sense of not assuming that the reader has had substantial previous exposure to the subject), but impart from the very beginning a rather modern, categorically-minded viewpoint, and aim at reaching a good level of depth. Many textbooks in algebra satisfy brilliantly some, but not all of these requirements. This book is my attempt at providing a working alternative.

There is a widespread perception that categories should be avoided at first blush, that the abstract language of categories should not be introduced until a student has toiled for a few semesters through example-driven illustrations of the nature of a subject like algebra. According to this viewpoint, categories are only tangentially relevant to the main topics covered in a beginning course, so they can simply be mentioned occasionally for the general edification of a reader, who will in time learn about them (by osmosis?). Paraphrasing a reviewer of a draft of the present text, ‘Discussions of categories at this level are the reason why God created appendices’.

It will be clear from a cursory glance at the table of contents that I think otherwise. In this text, categories are introduced around p. 20, after a scant reminder of the basic language of naive set theory, for the main purpose of providing a context for universal properties. These are in turn evoked constantly as basic definitions are introduced. The word ‘universal’ appears at least 100 times in the first three chapters.

If you are interested in a category theory based introduction to algebra, this may be the text for you. Suitable (according to the author) for use in a classroom or for self-study.

The ability to reason carefully, about what we imagine is known, should not be underestimated.

I first saw this in a tweet from Algebra Fact.

Powered by WordPress