Entropy Explained, With Sheep by Aatish Bhatia.
Entropy is relevant to information theory, encryption, Shannon, but I mention it here because of the cleverness of the explanation.
Aatish sets a very high bar for taking a difficult concept and creating a compelling explanation that does not involve hand-waving and/or leaps of faith on the part of the reader.
Highly recommended as a model for explanation!
Enjoy!
Quantum Shannon Theory by John Preskill.
Abstract:
This is the 10th and final chapter of my book on Quantum Information, based on the course I have been teaching at Caltech since 1997. An early version of this chapter (originally Chapter 5) has been available on the course website since 1998, but this version is substantially revised and expanded. The level of detail is uneven, as I’ve aimed to provide a gentle introduction, but I’ve also tried to avoid statements that are incorrect or obscure. Generally speaking, I chose to include topics that are both useful to know and relatively easy to explain; I had to leave out a lot of good stuff, but on the other hand the chapter is already quite long. This is a working draft of Chapter 10, which I will continue to update. See the URL on the title page for further updates and drafts of other chapters, and please send me an email if you notice errors. Eventually, the complete book will be published by Cambridge University Press.
Prekill tweeted requesting reviews of and comments on this 112 page “chapter” from Quantum Information (forthcoming, appropriately, no projected date).
Be forewarned that Preskill compresses classical information theory into 14 pages or so. 😉
You can find more chapters at: Quantum Computation.
Previous problem sets with solutions are also available.
Quantum computing is coming. Are you going to be the first quantum hacker?
Enjoy!
Visual Information Theory by Christopher Olah.
From the post:
I love the feeling of having a new way to think about the world. I especially love when there’s some vague idea that gets formalized into a concrete concept. Information theory is a prime example of this.
Information theory gives us precise language for describing a lot of things. How uncertain am I? How much does knowing the answer to question A tell me about the answer to question B? How similar is one set of beliefs to another? I’ve had informal versions of these ideas since I was a young child, but information theory crystallizes them into precise, powerful ideas. These ideas have an enormous variety of applications, from the compression of data, to quantum physics, to machine learning, and vast fields in between.
Unfortunately, information theory can seem kind of intimidating. I don’t think there’s any reason it should be. In fact, many core ideas can be explained completely visually!
Great visualization of the central themes of information theory!
Plus an interesting aside at the end of the post:
Claude Shannon’s original paper on information theory, A Mathematical Theory of Computation, is remarkably accessible. (This seems to be a recurring pattern in early information theory papers. Was it the era? A lack of page limits? A culture emanating from from Bell Labs?)
Cover & Thomas’ Elements of Information Theory seems to be the standard reference. I found it helpful.
Cover & Thomas’ Elements of Information Theory
I don’t find Shannon’s “accessibility” all that remarkable, he was trying to be understood. Once a field matures and develops an insider jargon, trying to be understood is no longer “professional.” Witness the lack of academic credit for textbooks and other explanatory material as opposed to jargon-laden articles that may or may not be read by anyone other than proof readers.
Musical Genres Classified Using the Entropy of MIDI Files (Emerging Technology from the arXiv, October 15, 2015)
Communication is the process of reproducing a message created in one point space at another point in space. It has been studied in depth by numerous scientists and engineers but it is the mathematical treatment of communication that has had the most profound influence.
To mathematicians, the details of a message are of no concern. All that matters is that the message can be thought of as an ordered set of symbols. Mathematicians have long known that this set is governed by fundamental laws first outlined by Claude Shannon in his mathematical theory of communication.
Shannon’s work revolutionized the way engineers think about communication but it has far-reaching consequences in other areas, too. Language involves the transmission of information from one individual to another and information theory provides a window through which to study and understand its nature. In computing, data is transmitted from one location to another and information theory provides the theoretical bedrock that allows this to be done most efficiently. And in biology, reproduction can be thought of as the transmission of genetic information from one generation to the next.
Music too can be thought of as the transmission of information from one location to another, but scientists have had much less success in using information theory to characterize music and study its nature.
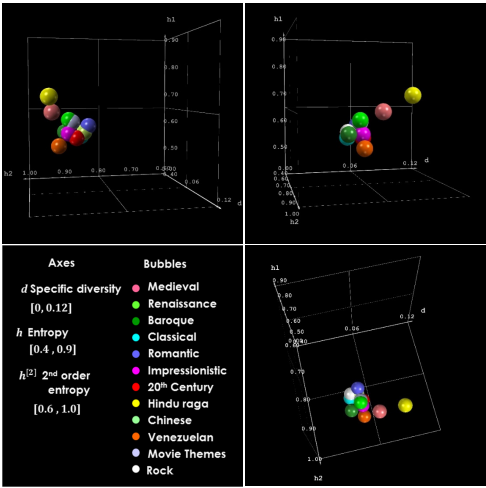
Today, that changes thanks to the work of Gerardo Febres and Klaus Jaffé at Simon Bolivar University in Venezuela. These guys have found a way to use information theory to tease apart the nature of certain types of music and to automatically classify different musical genres, a famously difficult task in computer science.
One reason why music is so hard to study is that it does not easily translate into an ordered set of symbols. Music often consists of many instruments playing different notes at the same time. Each of these can have various qualities of timbre, loudness, and so on.
…
Music viewed by its Entropy content: A novel window for comparative analysis by Gerardo Febres and Klaus Jaffe.
Abstract:
Texts of polyphonic music MIDI files were analyzed using the set of symbols that produced the Fundamental Scale (a set of symbols leading to the Minimal Entropy Description). We created a space to represent music pieces by developing: (a) a method to adjust a description from its original scale of observation to a general scale, (b) the concept of higher order entropy as the entropy associated to the deviations of a frequency ranked symbol profile from a perfect Zipf profile. We called this diversity index the “2nd Order Entropy”. Applying these methods to a variety of musical pieces showed how the space “symbolic specific diversity-entropy – 2nd order entropy” captures some of the essence of music types, styles, composers and genres. Some clustering around each musical category is shown. We also observed the historic trajectory of music across this space, from medieval to contemporary academic music. We show that description of musical structures using entropy allows to characterize traditional and popular expressions of music. These classification techniques promise to be useful in other disciplines for pattern recognition, machine learning, and automated experimental design for example.
The process simplifies the data stream, much like you choose which subjects you want to talk about in a topic map.
Purists will object but realize that objection is because they have chosen a different (and much more complex) set of subjects to talk about in the analysis of music.
The important point is to realize we are always choosing different degrees of granularity of subjects and their identifications, for some specific purpose. Change that purpose and the degree of granularity will change.
Communicating and resolving entity references by R.V. Guha.
Abstract:
Statements about entities occur everywhere, from newspapers and web pages to structured databases. Correlating references to entities across systems that use different identifiers or names for them is a widespread problem. In this paper, we show how shared knowledge between systems can be used to solve this problem. We present “reference by description”, a formal model for resolving references. We provide some results on the conditions under which a randomly chosen entity in one system can, with high probability, be mapped to the same entity in a different system.
An eye appointment is going to prevent me from reading this paper closely today.
From a quick scan, do you think Guha is making a distinction between entities and subjects (in the topic map sense)?
What do you make of literals having no identity beyond their encoding? (page 4, #3)
Redundant descriptions? (page 7) Would you say that defining a set of properties that must match would qualify? (Or even just additional subject indicators?)
Expect to see a lot more comments on this paper.
Enjoy!
I first saw this in a tweet by Stefano Bertolo.
From Classical to Quantum Shannon Theory by Mark M. Wilde
Abstract:
The aim of this book is to develop “from the ground up” many of the major, exciting, pre- and post-millenium developments in the general area of study known as quantum Shannon theory. As such, we spend a significant amount of time on quantum mechanics for quantum information theory (Part II), we give a careful study of the important unit protocols of teleportation, super-dense coding, and entanglement distribution (Part III), and we develop many of the tools necessary for understanding information transmission or compression (Part IV). Parts V and VI are the culmination of this book, where all of the tools developed come into play for understanding many of the important results in quantum Shannon theory.
From Chapter 1:
You may be wondering, what is quantum Shannon theory and why do we name this area of study as such? In short, quantum Shannon theory is the study of the ultimate capability of noisy physical systems, governed by the laws of quantum mechanics, to preserve information and correlations. Quantum information theorists have chosen the name quantum Shannon theory to honor Claude Shannon, who single-handedly founded the fi eld of classical information theory, with a groundbreaking 1948 paper [222]. In particular, the name refers to the asymptotic theory of quantum information, which is the main topic of study in this book. Information theorists since Shannon have dubbed him the “Einstein of the information age.”1 The name quantum Shannon theory is fit to capture this area of study because we use quantum versions of Shannon’s ideas to prove some of the main theorems in quantum Shannon theory.
This is of immediate importance if you are interested in current research in information theory. Of near-term importance if you are interested in practical design of algorithms for quantum information systems.
Powered by WordPress