Monte-Carlo Tree Search for Multi-Player Games by Joseph Antonius Maria Nijssen.
From the introduction:
The topic of this thesis lies in the area of adversarial search in multi-player zero-sum domains, i.e., search in domains having players with conflicting goals. In order to focus on the issues of searching in this type of domains, we shift our attention to abstract games. These games provide a good test domain for Artificial Intelligence (AI). They offer a pure abstract competition (i.e., comparison), with an exact closed domain (i.e., well-defined rules). The games under investigation have the following two properties. (1) They are too complex to be solved with current means, and (2) the games have characteristics that can be formalized in computer programs. AI research has been quite successful in the field of two-player zero-sum games, such as chess, checkers, and Go. This has been achieved by developing two-player search techniques. However, many games do not belong to the area where these search techniques are unconditionally applicable. Multi-player games are an example of such domains. This thesis focuses on two different categories of multi-player games: (1) deterministic multi-player games with perfect information and (2) multi-player hide-and-seek games. In particular, it investigates how Monte-Carlo Tree Search can be improved for games in these two categories. This technique has achieved impressive results in computer Go, but has also shown to be beneficial in a range of other domains.
This chapter is structured as follows. First, an introduction to games and the role they play in the field of AI is provided in Section 1.1. An overview of different game properties is given in Section 1.2. Next, Section 1.3 defines the notion of multi-player games and discusses the two different categories of multi-player games that are investigated in this thesis. A brief introduction to search techniques for two-player and multi-player games is provided in Section 1.4. Subsequently, Section 1.5 defines the problem statement and four research questions. Finally, an overview of this thesis is provided in Section 1.6.
This thesis is great background reading on the use of Monte-Carol tree search in games. While reading the first chapter, I realized that assigning semantics to a token is an instance of a multi-player game with hidden information. That is the “semantic” of any token doesn’t exist in some Platonic universe but rather is the result of some N number of players who also accept a particular semantic for some given token in a particular context. And we lack knowledge of the semantic and the reasons for it that will be assigned by some N number of players, which may change over time and context.
The semiotic triangle of Ogden and Richards (The Meaning of Meaning):
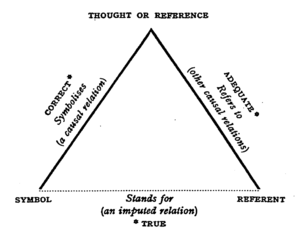
for any given symbol, represents the view of a single speaker. But as Ogden and Richards note, what is heard by listeners should be represented by multiple semiotic triangles:
Normally, whenever we hear anything said we spring spontaneously to an immediate conclusion, namely, that the speaker is referring to what we should be referring to were we speaking the words ourselves. In some cases this interpretation may be correct; this will prove to be what he has referred to. But in most discussions which attempt greater subtleties than could be handled in a gesture language this will not be so. (The Meaning of Meaning, page 15 of the 1923 edition)
Is RDF/OWL more subtle than can be handled by a gesture language? If you think so then you have discovered one of the central problems with the Semantic Web and any other universal semantic proposal.
Not that topic maps escape a similar accusation, but with topic maps you can encode additional semiotic triangles in an effort to avoid confusion, at least to the extent of funding and interest. And if you aren’t trying to avoid confusion, you can supply semiotic triangles that reach across understandings to convey additional information.
You can’t avoid confusion altogether nor can you achieve perfect communication with all listeners. But, for some defined set of confusions or listeners, you can do more than simply repeat your original statements in a louder voice.
Whether Monte-Carlo Tree searches will help deal with the multi-player nature of semantics isn’t clear but it is an alternative to repeating “…if everyone would use the same (my) system, the world would be better off…” ad nauseam.
I first saw this in a tweet by Ebenezer Fogus.