Rethinking set theory by Tom Leinster.
From the introduction:
Mathematicians manipulate sets with con�fidence almost every day of their working lives. We do so whenever we work with sets of real or complex numbers, or with vector spaces, topological spaces, groups, or any of the many other set-based structures. These underlying set-theoretic manipulations are so automatic that we seldom give them a thought, and it is rare that we make mistakes in what we do with sets.
However, very few mathematicians could accurately quote what are often referred to as `the’ axioms of set theory. We would not dream of working with, say, Lie algebras without �first learning the axioms. Yet many of us will go our whole lives without learning `the’ axioms for sets, with no harm to the accuracy of our work. This suggests that we all carry around with us, more or
less subconsciously, a reliable body of operating principles that we use when manipulating sets.
What if we were to write down some of these principles and adopt them as our axioms for sets? The message of this article is that this can be done, in a simple, practical way. We describe an
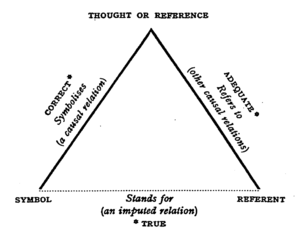
axiomatization due to F. William Lawvere [3, 4], informally summarized in Fig. 1. The axioms suffi�ce for very nearly everything mathematicians ever do with sets. So we can, if we want, abandon the classical axioms entirely and use these instead.
…
Don’t try to read this after a second or third piece of pie. 😉
What captured my interest was the following:
The root of the problem is that in the frame-work of ZFC, the elements of a set are always sets too. Thus, given a set X, it always makes sense in ZFC to ask what the elements of the elements of X; are. Now, a typical set in ordinary mathematics is ℝ. But accost a mathematician at random and ask them `what are the elements of Π?’, and they will probably assume they misheard you, or ask you what you’re talking about, or else tell you that your question makes no sense. If forced to answer, they might reply that real numbers have no elements. But this too is in conflict with ZFC’s usage of `set’: if all elements of ℝ are sets, and they all have no elements, then they are all the empty set, from which it follows that all real numbers are equal. (emphasis added)
The author explores the perils of using “set” with two different meanings in ZFC and what it could mean to define “set” as it is used in practice by mathematicians.
For my part, the “…elements of a set are always sets too” resonates with the concept that all identifiers can be resolved into identifiers.
For example: firstName = Patrick.
The token firstName, despite its popularity on customs forms, is not a semantic primitive recognized by all readers. While for some processing purposes, by agents hired to delay, harass and harry tired travelers, firstName is sufficient, it can in fact be resolved into tuples that represent equivalences to firstName or provide additional information about that identifier.
For example:
name = "firstName"
alt = "given name"
alt = "forename"
alt = "Christian name"
Which slightly increases my chances of finding an equivalent, if I am not familiar with firstName. I say “slightly increases” because names of individual people are subject to a rich heritage of variation based on language, culture, custom, all of which have changed over time. The example is just a tiny number of possible alternatives possible in English.
When I say “…it can in fact be resolved…” should not be taken to require that every identifier be so resolved or that the resulting identifiers extend to some particular level of resolution. Noting that we could similarly expand forename or alt and the identifiers we find in their expansions.
The question that a topic maps designer has to answer is “what expansions of identifiers are useful for a particular set of uses?” Do the identifiers need to survive their current user? (Think legacy ETL.) Will the data need to be combined with data using other identifiers? Will queries need to be made across data sets with conflicting identifiers? Is there data that could be merged on a subject by subject basis? Is there any value in a subject by subject merging?
To echo a sentiment that I heard in Leading from the Back: Making Data Science Work at a UX-driven Business, it isn’t the fact you can merge information about a subject that’s important. It is the value-add to a customer that results from that merging that is important.
Value-add for customers before toys for IT.*
I first saw this in a tweet by onepaperperday.
*This is a tough one for me, given my interests in language and theory. But I am trying to do better.